
Calinon, S., Guenter, F. and Billard, A. (2007)
On Learning, Representing and Generalizing a Task in a Humanoid Robot
IEEE Transactions on Systems, Man and Cybernetics, Part B, Special issue on robot learning by observation, demonstration and imitation, 37:2, 286-298.
Abstract
We present a Programming by Demonstration (PbD) framework for generically extracting the relevant features of a given task and for addressing the problem of generalizing the acquired knowledge to different contexts. We validate the architecture through a series of experiments in which a human demonstrator teaches a humanoid robot some simple manipulatory tasks. A probability based estimation of the relevance is suggested, by first projecting the joint angles, hand paths, and object-hand trajectories onto a generic latent space using Principal Component Analysis (PCA). The resulting signals were then encoded using a mixture of Gaussian/Bernoulli distributions (GMM/BMM). This provides a measure of the spatio-temporal correlations across the different modalities collected from the robot which can be used to determine a metric of the imitation performance. The trajectories are then generalized using Gaussian Mixture Regression (GMR). Finally, we analytically compute the trajectory which optimizes the imitation metric and use this to generalize the skill to different contexts and to the robot's specific bodily constraints.
Bibtex reference
@article{Calinon07,
author="S. Calinon and F. Guenter and A. Billard",
title="On Learning, Representing and Generalizing a Task in a Humanoid Robot",
journal="{IEEE} Transactions on Systems, Man and Cybernetics, Part {B}. {S}pecial issue
on robot learning by observation, demonstration and imitation",
year="2007",
volume="37",
number="2",
pages="286--298"
}
Video
Learning of a chess move by observing multiple demonstrations starting from different initial positions on the chessboard. The robot is then able to generalize and reproduce the task in new situations (new initial position) that has not been observed during the demonstrations.
Source codes
Download
Usage
Unzip the file and run 'demo1', 'demo2' or 'demo3' in Matlab.
References
- Calinon, S., Guenter, F. and Billard, A. (2007) On Learning, Representing and Generalizing a Task in a Humanoid Robot. IEEE Transactions on Systems, Man and Cybernetics, Part B. 37:2, 286-298.
Demo 1 - Demonstration of the generalization process using Gaussian Mixture Regression (GMR)
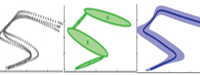
The program loads a 3D dataset, trains a Gaussian Mixture Model (GMM), and retrieves a generalized version of the dataset with associated constraints through Gaussian Mixture Regression (GMR). Each datapoint has 3 dimensions, consisting of 1 temporal value and 2 spatial values (e.g., drawing on a 2D Cartesian plane). A sequence of temporal values is used as query points to retrieve a sequence of expected spatial distribution through Gaussian Mixture Regression (GMR).
Demo 2 - Demonstration of Gaussian Mixture Regression (GMR) using spatial components as query points of arbitrary dimensions
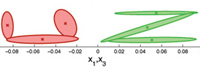
The programs loads a 4D dataset, trains a Gaussian Mixture Model (GMM), and uses query points of 2 dimensions to retrieve a generalized version of the data for the remaining 2 dimensions, with associated constraints, through Gaussian Mixture Regression (GMR). Each datapoint has 4 dimensions, consisting of 2x2 spatial values (e.g., drawing on a 2D Cartesian plane simultaneously with right and left hand). A new sequence of 2D spatial values (data for left hand) is loaded and used as query points to retrieve a sequence of expected spatial distribution for the remaining dimensions (data for right hand), through Gaussian Mixture Regression (GMR).
Demo 3 - Demonstration of the smooth transitions properties of data retrieved by Gaussian Mixture Regression (GMR)
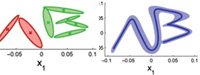
This program loads two 3D datasets, trains two separates Gaussian Mixture Model (GMM), and retrieves a generalized version of the two datasets concatenated in time, with associated constraints, through Gaussian Mixture Regression (GMR). Each datapoint has 3 dimensions, consisting of 1 temporal value and 2 spatial values (e.g., drawing on a 2D Cartesian plane). A sequence of temporal values is used as query points to retrieve a sequence of expected spatial distribution through Gaussian Mixture Regression (GMR). The position of the last datapoint in the first dataset is not consistent with the first datapoint of the second dataset. However, by encoding separately the two datasets in GMM and concatenating the components in a single model, a smooth signal with smooth transition between the two data is retrieved through regression.
 Â
Â