Li, Y. and Calinon, S. (2025)
From Movement Primitives to Distance Fields to Dynamical Systems
arXiv:2504.09705.
Abstract
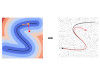
Developing autonomous robots capable of learning and reproducing complex motions from demonstrations remains a fundamental challenge in robotics. On the one hand, movement primitives (MPs) provide a compact and modular representation of continuous trajectories. On the other hand, autonomous systems provide control policies that are time independent. We propose in this paper a simple and flexible approach that gathers the advantages of both representations by transforming MPs into autonomous systems. The key idea is to transform the explicit representation of a trajectory as an implicit shape encoded as a distance field. This conversion from a time-dependent motion to a spatial representation enables the definition of an autonomous dynamical system with modular reactions to perturbation. Asymptotic stability guarantees are provided by using Bernstein basis functions in the MPs, representing trajectories as concatenated quadratic Bézier curves, which provide an analytical method for computing distance fields. This approach bridges conventional MPs with distance fields, ensuring smooth and precise motion encoding, while maintaining a continuous spatial representation. By simply leveraging the analytic gradients of the curve and its distance field, a stable dynamical system can be computed to reproduce the demonstrated trajectories while handling perturbations, without requiring a model of the dynamical system to be estimated. Numerical simulations and real-world robotic experiments validate our method's ability to encode complex motion patterns while ensuring trajectory stability, together with the flexibility of designing the desired reaction to perturbations.
Bibtex reference
@article{Li25arXiv,
author={Li, Y. and Calinon, S.},
title={From Movement Primitives to Distance Fields to Dynamical Systems},
journal={arXiv:2504.09705},
year={2025}
}